まとめ
課税所得から税額を求めるときの税率は、掛ける数(見かけの税率)の方が注目されることが多く、例えば課税所得4千万円以上の税率は45%といわれたりしますが、実際には課税所得毎に決まっている数を掛けた後に、課税所得毎に決まっている数を引いているので、課税所得毎に税率(税額/課税所得)は異なっています。
例えば、課税所得4千万円では、実際の税率は、(40000000*0.45-4796000)/40000000 = 0.3301なので、約33%です。
所得税の課税所得と正味の税率の関係をグラフに表示すると以下のようになります。
- ピンク線: 課税所得に掛けられているいわゆる税率
- 赤線: 所定の額を引いた後の正味の税率
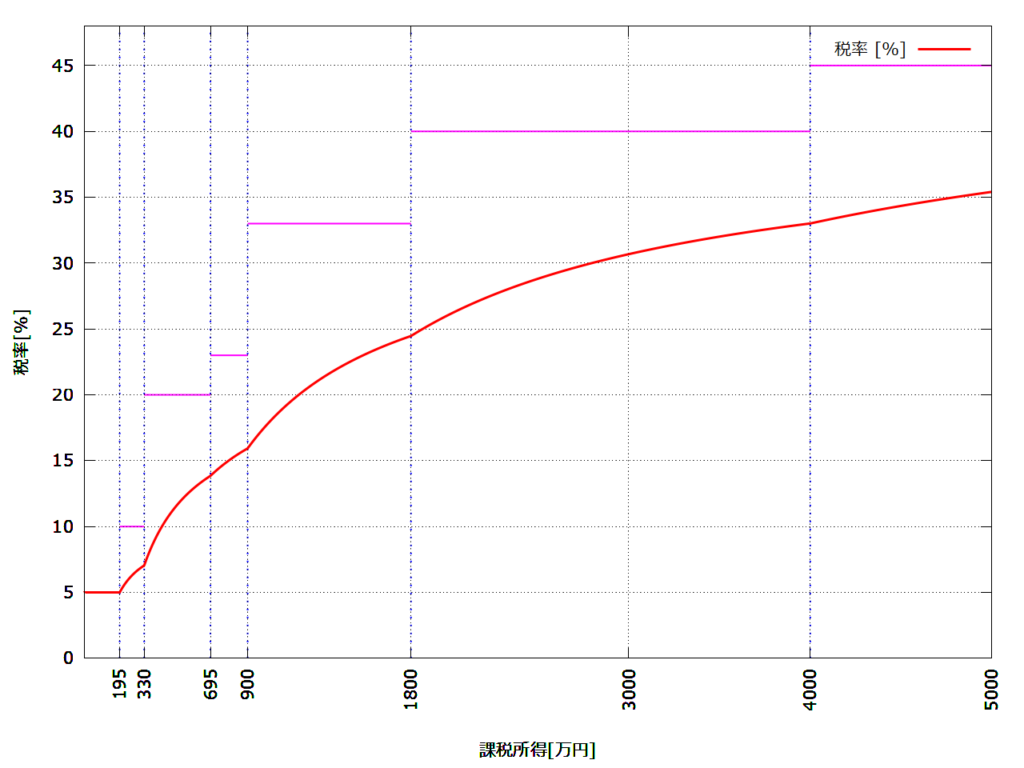
課税所得のレベル毎に一定の額が引かれますので、正味の税率の上がり方は、レベルが上がった直後に傾きが大きく、次にレベルが上がる直前は傾きが小さくなります。レベルが上がった直後あたりは損ともいえますが、連続に変化しているので大きな違いはないともいえます。節税には、下のレベルの課税所得にこだわるよりも、課税所得額によって制限される手当てや補助の影響が大きいように思われます。
説明
所得税は課税される所得金額(課税所得)に対して、税率が変動する累進課税ですが、課税所得に対して掛ける値「見かけの税率」だけではなく、税率をかけた後に「引く額」も変わっているため、実際の税率(税額/課税所得)が見えづらくなっています。税額は以下の形になっています。
税額 = 課税所得金額 × 「見かけの税率」 – 「引く額」
(「正味の税率」,「見かけの税率」,「引く額」はわかりやすいようにここでつけたことばです)
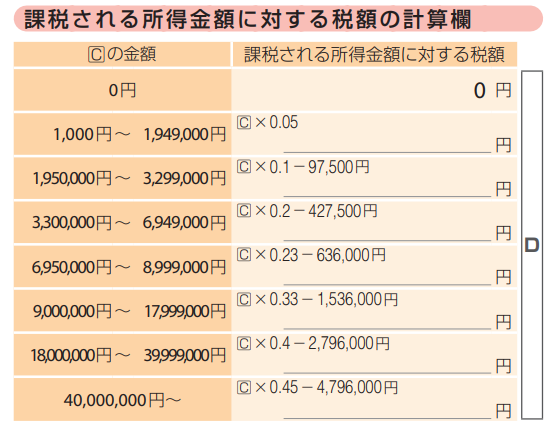
「引く額」が入っていることで正味の税率が見えづらくなっているので、「引く額」を含めた税率をグラフにしてみました。
超過累進課税
ちなみに、「引く額」は「超過累進課税」にするためにあります。「超過累進課税」とは、
195万までは5%,
195~330万は10%,
…,
4000万を超える分には45%
という税率で計算するものです。
(以上のように計算するので表の行が変化したときでも税額・税率は連続になります)
「超過累進課税」では、課税所得4000万円以上の税率が45%というのは、正しくは「課税所得-4000万円」に対する税率が45%ということです。
たとえば、500万の課税所得に対する税額を「超過累進課税」で求めてみると、
(以下で*は×を意味します)
0~195万は5% = (195-0)*0.05 = 9.75万
195~330万は10% = (330-195)*0.1 = 13.5万
330~500万は20% = (500-330)*0.2 = 34万
計 9.75万+13.5万+34万 = 57.25万ですが、
表の通りに計算しても 500*0.2-42.75= 57.25万 となります。
課税所得が330~650万を例にとって「引く額」の求め方を説明します。
D: 税額
C: 課税所得
α: 引く額
とすると、330万以上の税率は0.2なので、D = 0.2 C + α となります。
C: 330~650万でαは一定なので、C==330万で計算すると、
D = 9.75+13.5 = 0.2*330 + α より
α = (9.75 + 13.5) – 0.2*330 = -42.75
からC:330~650万のときの「引く額」の-42.75が求められます。
同様の計算でそれぞれの「引く額」が求められます。
課税所得>=4000万についての「引く額」は、同様の計算で以下のように求められます。
(195-0)*0.05+(330-195)*0.1+(695-330)*0.2+(900-695)*0.23+(1800-900)*0.33+(4000-1800)*0.4 – 0.45*4000 = -479.6
「正味の税率」は上のグラフのとおりですが、「超過累進課税」であることを知っていれば、例えば、ある時点の課税所得が340万で経費を使うときに、課税所得が330万以上で税率20%、330万以下で10%なので、税額は、経費10万(課税所得330万)までは経費の20%で減っていくが、そこからは課税所得が195万になるまでは10%で減っていくということがわかります。
三項演算子について
グラフはgnuplotというソフトで三項演算子を使って作成しています。
この記事は、確定申告の時期で税金の話をしているように見えて、実は三項演算子の有効な使い方を示すための記事です(作成したグラフは実際の課税所得に対する所得税率をあらわしています)。確定申告の時期ということもあり例として課税所得と正味の税率を計算してみました。
三項演算子が存在するプログラム言語は多いですが、使ってみると読みづらく(可読性が落ちる)、使い所がいま一つありません。
三項演算子の有効な使い方は何かと考えた場合、定義域によって数式が変化するものを記述するときに有効でした。
例えば、上の表から税額を表す関数D(x)をgnuplotで三項演算子を使って表すと以下のようになります。(課税所得は1,000円刻みですが、以下では定義域を網羅するように修正してあります)
D(x) = \
( x< 1000.0) ? 0 : \
( 1000.0<=x && x< 1950000.0) ? x*0.05 : \
( 1950000.0<=x && x< 3300000.0) ? x*0.10 - 97500 : \
( 3300000.0<=x && x< 6950000.0) ? x*0.20 - 427500 : \
( 6950000.0<=x && x< 9000000.0) ? x*0.23 - 636000 : \
( 9000000.0<=x && x< 18000000.0) ? x*0.33 - 1536000 : \
( 18000000.0<=x && x< 40000000.0) ? x*0.40 - 2796000 : \
x*0.45 - 4796000 ほぼ、上の表と同じ形に書けるので、書くのも読むのも楽で、修正しやすく、間違いが起きづらいと思います。税率はD(x)/xとなります。
また、このように記述すると、このような表が多段(前の表の出力が次の表の入力)になっていて、表ごとに定義域が異なっている場合でも容易に記述することができます。
最後に、上のグラフをpngで保存するgnuplotのスクリプトを載せておきます。縦の青点線・横のピンク線を描くために行数が増えていますが、赤い線を描いているのは1行です。スクリプトはUTF-8で保存します。
set encoding utf8
# 課税される所得金額に対する税額の計算
# 「令和5年分所得税及び復興特別所得税の手引き.pdf」p.24より
# C:x
D(x) = \
( x< 1000.0) ? 0 : \
( 1000.0<=x && x< 1950000.0) ? x*0.05 : \
( 1950000.0<=x && x< 3300000.0) ? x*0.10 - 97500 : \
( 3300000.0<=x && x< 6950000.0) ? x*0.20 - 427500 : \
( 6950000.0<=x && x< 9000000.0) ? x*0.23 - 636000 : \
( 9000000.0<=x && x< 18000000.0) ? x*0.33 - 1536000 : \
( 18000000.0<=x && x< 40000000.0) ? x*0.40 - 2796000 : \
x*0.45 - 4796000
set samp 1000
# p [0.0:5000.0] D(10000.0*x)
set grid
set xlabel '課税所得[万円]'
set ylabel '税率[%]'
set term pngcairo size 1280,960 font "Meiryo,16.0"
set out 'tax_rate.png'
set multi
set param
set trange [0:48]
set xrange [0:5000]
set xtics rotate (195,330,695, 900, 1800, 3000, 4000, 5000)
set yrange [0:48]
p 195,t lc 3 lw 2 dt 3 t ''
p 330,t lc 3 lw 2 dt 3 t ''
p 695,t lc 3 lw 2 dt 3 t ''
p 900,t lc 3 lw 2 dt 3 t ''
p 1800,t lc 3 lw 2 dt 3 t ''
p 4000,t lc 3 lw 2 dt 3 t ''
set trange [195:330]
p t,10 lc 4 lw 2 t ''
set trange [330:695]
p t,20 lc 4 lw 2 t ''
set trange [695:900]
p t,23 lc 4 lw 2 t ''
set trange [900:1800]
p t,33 lc 4 lw 2 t ''
set trange [1800:4000]
p t,40 lc 4 lw 2 t ''
set trange [4000:5000]
p t,45 lc 4 lw 2 t ''
unset param
p [0.0:5000.0] D(10000.0*x)/(10000.0*x)*100 lw 3 t '税率 [%]'
unset multi
set out
set term win
以上
コメント